C++中实现动态多维数组模板的分析-04 - 悲催的科学匠人 - 冷水's blog
C++中实现动态多维数组模板的分析-04
冷水
posted @ 2010年12月17日 00:52
in C++
, 1364 阅读
对于一维化存储的数据,实现多维编号访问,索引是必须的。
考虑2D数组 array[0..I-1][0..J-1],为了方便采用FORTRAN的数组元素排列顺序,即
for (j=0;j<J;j++) for (i=0;i<I;i++)
那么一维编号
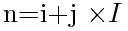
为了避免乘法,我们可以预先计算好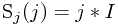 。则有一维编号计算公式为
。则有一维编号计算公式为
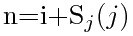
代价是我们必须事先计算好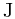 个
个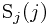 。
。
再考虑3D数组 array[0..I-1][0..J-1][0..K-1],其一维编号计算公式为
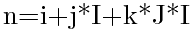
同理,令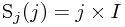 和
和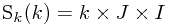 ,上式可写为
,上式可写为
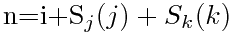
这个方法可以推导到任意维数组。即对于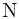 维数组,设其第
维数组,设其第 维范围是
维范围是![$\left[ 0 \dots D_i-1 \right ] $ $\left[ 0 \dots D_i-1 \right ] $](/user_files/quaintchewster/epics/0f7a129d4a3f03266ced132b472de8eed805e560.png) ,我们事先计算好偏移
,我们事先计算好偏移
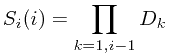
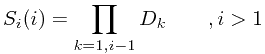
此外对于第一维

则元素![$[k_1][k_2]\dots[k_i]\dots[k_N]$ $[k_1][k_2]\dots[k_i]\dots[k_N]$](/user_files/quaintchewster/epics/19db29720ef3e3b71df887347bde906f290480ea.png) 的一维编号计算格式为
的一维编号计算格式为
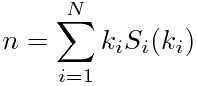
这样对于多维数组![$A[N_1][N_2]\dots[N_n]$ $A[N_1][N_2]\dots[N_n]$](/user_files/quaintchewster/epics/b126e87837c01e0ea6b1b6194ce20703dbedbf41.png) ,只需要实现计算好
,只需要实现计算好 个常数,即可采用上式来快速计算一维编号。
个常数,即可采用上式来快速计算一维编号。
 评论 (0)
评论 (0)