悲催的科学匠人 - 冷水's blog

[zz]FORTRAN版非递归快速排序

在二叉树离散网格单元时，最初使用递归的，但是网格单元到百万量级时，排序程序就出错了。怀疑是递归耗尽系统堆栈的问题，搜到一个非递归版本： http://www.fortran.com/fortran/quick_sort2.f 百万量级也不是问题了。

      PROGRAM test_nrqsort
      REAL,ALLOCATABLE :: array(:)
      INTEGER,ALLOCATABLE :: idx(:)
      INTEGER N,i
      INTEGER,PARAMETER :: seed = 86456
      
      !READ(*,*) N
      N = 5000000
      ALLOCATE(array(N),idx(N))
      CALL srand(seed)
      DO i=1,N; 
         array(i) = rand()
      ENDDO
      WRITE(*,*) 'sorting'
      CALL SORTRX(N,array,idx)
      !DO i=1,N
      !  WRITE(*,*) array(idx(i))
      !ENDDO
      DO i=2,N
      IF(array(idx(i)) .lt. array(idx(i-1)) ) THEN
        WRITE(*,*) 'error', array(idx(i)), array(idx(i-1))
      ENDIF
      ENDDO
      DEALLOCATE(array,idx)
      END

C From Leonard J. Moss of SLAC:

C Here's a hybrid QuickSort I wrote a number of years ago.  It's
C based on suggestions in Knuth, Volume 3, and performs much better
C than a pure QuickSort on short or partially ordered input arrays.  

      SUBROUTINE SORTRX(N,DATA,INDEX)
C===================================================================
C
C     SORTRX -- SORT, Real input, indeX output
C
C
C     Input:  N     INTEGER
C             DATA  REAL
C
C     Output: INDEX INTEGER (DIMENSION N)
C
C This routine performs an in-memory sort of the first N elements of
C array DATA, returning into array INDEX the indices of elements of
C DATA arranged in ascending order.  Thus,
C
C    DATA(INDEX(1)) will be the smallest number in array DATA;
C    DATA(INDEX(N)) will be the largest number in DATA.
C
C The original data is not physically rearranged.  The original order
C of equal input values is not necessarily preserved.
C
C===================================================================
C
C SORTRX uses a hybrid QuickSort algorithm, based on several
C suggestions in Knuth, Volume 3, Section 5.2.2.  In particular, the
C "pivot key" [my term] for dividing each subsequence is chosen to be
C the median of the first, last, and middle values of the subsequence;
C and the QuickSort is cut off when a subsequence has 9 or fewer
C elements, and a straight insertion sort of the entire array is done
C at the end.  The result is comparable to a pure insertion sort for
C very short arrays, and very fast for very large arrays (of order 12
C micro-sec/element on the 3081K for arrays of 10K elements).  It is
C also not subject to the poor performance of the pure QuickSort on
C partially ordered data.
C
C Created:  15 Jul 1986  Len Moss
C
C===================================================================
 
      INTEGER   N,INDEX(N)
      REAL      DATA(N)
 
      INTEGER   LSTK(31),RSTK(31),ISTK
      INTEGER   L,R,I,J,P,INDEXP,INDEXT
      REAL      DATAP
 
C     QuickSort Cutoff
C
C     Quit QuickSort-ing when a subsequence contains M or fewer
C     elements and finish off at end with straight insertion sort.
C     According to Knuth, V.3, the optimum value of M is around 9.
 
      INTEGER   M
      PARAMETER (M=9)
 
C===================================================================
C
C     Make initial guess for INDEX
 
      DO 50 I=1,N
         INDEX(I)=I
   50    CONTINUE
 
C     If array is short, skip QuickSort and go directly to
C     the straight insertion sort.
 
      IF (N.LE.M) GOTO 900
 
C===================================================================
C
C     QuickSort
C
C     The "Qn:"s correspond roughly to steps in Algorithm Q,
C     Knuth, V.3, PP.116-117, modified to select the median
C     of the first, last, and middle elements as the "pivot
C     key" (in Knuth's notation, "K").  Also modified to leave
C     data in place and produce an INDEX array.  To simplify
C     comments, let DATA[I]=DATA(INDEX(I)).
 
C Q1: Initialize
      ISTK=0
      L=1
      R=N
 
  200 CONTINUE
 
C Q2: Sort the subsequence DATA[L]..DATA[R].
C
C     At this point, DATA[l] <= DATA[m] <= DATA[r] for all l < L,
C     r > R, and L <= m <= R.  (First time through, there is no
C     DATA for l < L or r > R.)
 
      I=L
      J=R
 
C Q2.5: Select pivot key
C
C     Let the pivot, P, be the midpoint of this subsequence,
C     P=(L+R)/2; then rearrange INDEX(L), INDEX(P), and INDEX(R)
C     so the corresponding DATA values are in increasing order.
C     The pivot key, DATAP, is then DATA[P].
 
      P=(L+R)/2
      INDEXP=INDEX(P)
      DATAP=DATA(INDEXP)
 
      IF (DATA(INDEX(L)) .GT. DATAP) THEN
         INDEX(P)=INDEX(L)
         INDEX(L)=INDEXP
         INDEXP=INDEX(P)
         DATAP=DATA(INDEXP)
      ENDIF
 
      IF (DATAP .GT. DATA(INDEX(R))) THEN
         IF (DATA(INDEX(L)) .GT. DATA(INDEX(R))) THEN
            INDEX(P)=INDEX(L)
            INDEX(L)=INDEX(R)
         ELSE
            INDEX(P)=INDEX(R)
         ENDIF
         INDEX(R)=INDEXP
         INDEXP=INDEX(P)
         DATAP=DATA(INDEXP)
      ENDIF
 
C     Now we swap values between the right and left sides and/or
C     move DATAP until all smaller values are on the left and all
C     larger values are on the right.  Neither the left or right
C     side will be internally ordered yet; however, DATAP will be
C     in its final position.
 
  300 CONTINUE
 
C Q3: Search for datum on left >= DATAP
C
C     At this point, DATA[L] <= DATAP.  We can therefore start scanning
C     up from L, looking for a value >= DATAP (this scan is guaranteed
C     to terminate since we initially placed DATAP near the middle of
C     the subsequence).
 
         I=I+1
         IF (DATA(INDEX(I)).LT.DATAP) GOTO 300
 
  400 CONTINUE
 
C Q4: Search for datum on right <= DATAP
C
C     At this point, DATA[R] >= DATAP.  We can therefore start scanning
C     down from R, looking for a value <= DATAP (this scan is guaranteed
C     to terminate since we initially placed DATAP near the middle of
C     the subsequence).
 
         J=J-1
         IF (DATA(INDEX(J)).GT.DATAP) GOTO 400
 
C Q5: Have the two scans collided?
 
      IF (I.LT.J) THEN
 
C Q6: No, interchange DATA[I] <--> DATA[J] and continue
 
         INDEXT=INDEX(I)
         INDEX(I)=INDEX(J)
         INDEX(J)=INDEXT
         GOTO 300
      ELSE
 
C Q7: Yes, select next subsequence to sort
C
C     At this point, I >= J and DATA[l] <= DATA[I] == DATAP <= DATA[r],
C     for all L <= l < I and J < r <= R.  If both subsequences are
C     more than M elements long, push the longer one on the stack and
C     go back to QuickSort the shorter; if only one is more than M
C     elements long, go back and QuickSort it; otherwise, pop a
C     subsequence off the stack and QuickSort it.
 
         IF (R-J .GE. I-L .AND. I-L .GT. M) THEN
            ISTK=ISTK+1
            LSTK(ISTK)=J+1
            RSTK(ISTK)=R
            R=I-1
         ELSE IF (I-L .GT. R-J .AND. R-J .GT. M) THEN
            ISTK=ISTK+1
            LSTK(ISTK)=L
            RSTK(ISTK)=I-1
            L=J+1
         ELSE IF (R-J .GT. M) THEN
            L=J+1
         ELSE IF (I-L .GT. M) THEN
            R=I-1
         ELSE
C Q8: Pop the stack, or terminate QuickSort if empty
            IF (ISTK.LT.1) GOTO 900
            L=LSTK(ISTK)
            R=RSTK(ISTK)
            ISTK=ISTK-1
         ENDIF
         GOTO 200
      ENDIF
 
  900 CONTINUE
 
C===================================================================
C
C Q9: Straight Insertion sort
 
      DO 950 I=2,N
         IF (DATA(INDEX(I-1)) .GT. DATA(INDEX(I))) THEN
            INDEXP=INDEX(I)
            DATAP=DATA(INDEXP)
            P=I-1
  920       CONTINUE
               INDEX(P+1) = INDEX(P)
               P=P-1
               IF (P.GT.0) THEN
                  IF (DATA(INDEX(P)).GT.DATAP) GOTO 920
               ENDIF
            INDEX(P+1) = INDEXP
         ENDIF
  950    CONTINUE
 
C===================================================================
C
C     All done
 
      END

ExStream特性

大规模并行飞行器外流场分析工具 ExStream 特性简介

网格系统

支持1-1匹配式对接的多块结构化网格
支持重叠嵌套网格

数值方法

MUSCL插值和多种梯度限制器
JST格式与AUSM类格式
全梯度粘性通量与薄层假设粘性通量
几何多重网格与多级网格
显式Runge-Kutta时间推进与LUSGS隐式推进
双时间步长方法处理非稳态问题

流体属性

理想气体
基于Sutherland公式的粘性系数

湍流模型

k-Omega SST RANS模型
SA RANS模型
SA DES 分离流算法
SA DDES及其改进版本的分离流算法
SA IDDES 分离流算法
SA CLES 分离流算法

并行计算

基于MPI的对等式并行计算，主节点无显著额外负载及内存消耗
自动的网格切分和负载均衡
并行文件输入输出，支持2E63字节

输入

网格，mesh3d.dat，双精度三维多块PLOT3D格式，FORTRAN的unformat格式，只包含坐标数据，不包含IBLANK数据
边界信息，bc_in，边界类型与对接方式定义，可由ICEMCFD导出数据转换得到
基本求解控制参数，input，FORTRAN namelist格式
扩展模块的控制参数，usr.inp，FORTRAN namelist格式

输出

表面数据以文本tecpot格式输出，每个固体表面会标记其所属的部件名称，以便分类观察，p_surface.plt
体数据以PLOT3D格式给出，网格(mesh3dsp.dat)和数据(*.p3df)皆以单精度浮点数存储
各个部件的气动力以X-Y形式的tecplot格式提供，partforce.plt
残差收敛历史以X-Y形式的tecplot格式提供，res.dat
非稳态模拟的时间平均流场输出
非稳态下用户自定义监测点、监测块和面的输出

DPW-II表面压力分布

采用官方粗网格，单元数量约400万。

三角翼低速分离涡的DDES模拟

0.1马赫中等后掠角的三角翼，全模计算，网格单元约2000万

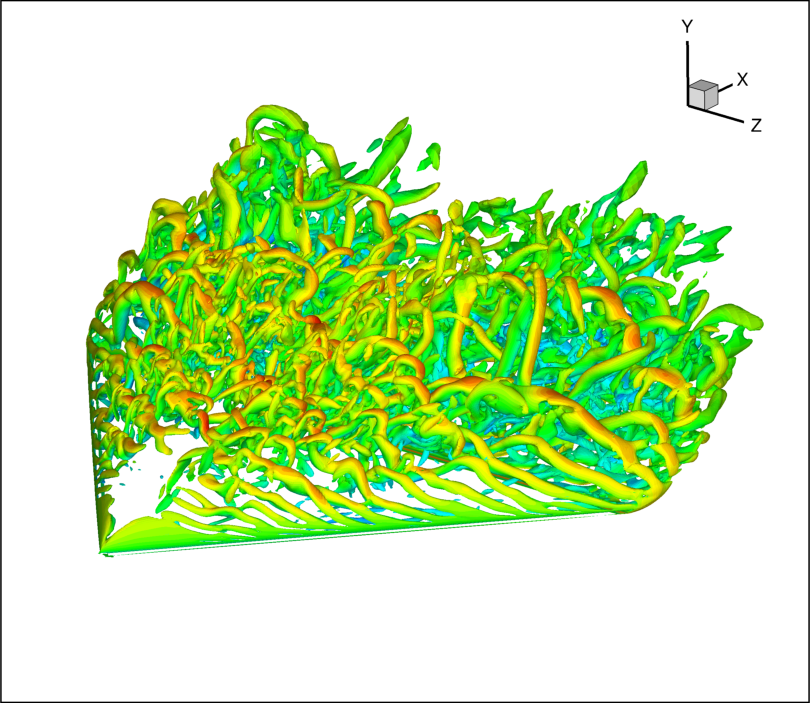
超声速底部流动的DDES模拟

来流马赫数为2.46，网格单元数约1000万。

天津超级计算中心天河-1A在linux下登录VPN的方法解释

原文见此链接

https://vpn.nscc-tj.cn/svpn/cn/support/OperationGuide%28Chinese%29.htm

在ubuntu下设置时，遇到几个问题

1 jre6的安装。ubuntu不再首选支持sun java，而推荐使用openjdk，因此软件库中没有sun java。为了保证兼容，还是选sun java吧。安装方法参考 https://help.ubuntu.com/community/Java 中关于Orancle(Sun) Java 6的部分

2 Firefox中设置JNLP文件打开方式。初始Firefox中没有JNLP文件选项，没法设置。方法是，自己建立一个空文件，后缀名为jnlp。把它拖到firefox中，firefox会提示打开方法，选择javaws。然后到首选项的application中就可以看到JNLP了，把它按照说明设置即可。

3 22端口问题。vpn客户端要占用22端口，只好把本机的ssh服务停了

4 root身份的问题。vpn客户端必须用root身份，但是在root环境下工作有风险。解决方法是，登录一个root桌面，登录好vpn之后，再切换登录一个普通用户桌面，就可以ssh到th-1a的三个登录节点了。

一个有用的网页注释工具

http://webklipper.com

可以指定一个URL，它生成一个拷贝。然后可以在页面上做各种标记和注释。可以把注释版分享给别人浏览或者合作添加注释。这玩意还可以支持自行上载文件(pdf、图形和txt)进行注释。

缺点：

1 似乎标记的位置不是根据文本的内容来定位，而是根据网页区域的坐标。因此改变窗口大小后，标记位置就错了

2 pdf会被转成图片格式，不清楚。

不论如何，这玩意还是很好的。非常适合多人剖析源代码之类的活。

« 上一页 1 2 3 4 5 6 7 8 9 10 11 12 13 下一页 »